
When the facts change, I change my mind. What do you do, Sir? – John Maynard Keynes
Bottom line
As we approach a return to clinical practice policy makers need to be mindful that the dental profession is already highly proficient in cross infection control, and the benefits of new elaborate PPE protocols regarding aerosol generating procedures may be marginal in the light of low disease prevalence. If we need 300,000 participants in a study it may be impossible to practically demonstrate significant benefits to patient safety from the perfect PPE model compared to the harms created by expense and access.
Background
The most important element of Keynes’s famous quote relating to the current coronavirus pandemic is the word ‘fact’. Facts at this moment in time are constantly changing as this disease spreads, and what was true two weeks ago is now a distant memory. One major problem we face as far as healthcare policy is concerned is a lack of accurate base-rate data on the prevalence of the disease in the population, this was initially addresses by Professor Ioannidis (Ioannidis, 2020). His article in STAT caused quite a lot of online controversy (Bastian, 2020, Taleb, 2020) but what it did is highlight the difficulties of being objective and human.
At this moment in time it is extremely difficult not to be influenced by the problems of base-rate neglect, loss aversion, and availability bias via the media as we count the daily international infection/death figures (Gaurav, 2020). In this post I want to concentrate on how important it is to understand the significance of accurate base-rate (prevalence) reporting so we can allocate the correct amount of training and resources to the dental profession based of the potential aerosol risk in virus transmission. In a paper by Chambers on base-rates in dental decision-making there is a quote (Chambers, 1999):
Base your decisions on either the baseline alone or the evidence alone, depending on which one contains the most information.
What we are seeing now is a rapid accumulation of both base-line data and evidence, but policy decisions about the future are being based on data and precautionary principles that were only valid at the start of this pandemic. To highlight this, I would like to explore how we are going to test the real-world effectiveness of the personal protective equipment (PPE) and cross infection protocols that are flooding the profession now.
Methods
I am going to look at three areas here, base-rates (prevalence), numbers of asymptomatic individuals, and power calculations regarding PPE use. For clarity I will use natural frequencies wherever possible.
Firstly, on the 14th May the Office of National Statistics (ONS) in the UK published the results of its coronavirus (Covid-19) infection survey (ONS, 2020). This data was based on 10,705 participants’ swab tests taken over a two-week period from 27th April to 10th May, the sample was drawn from households in which someone has already participated in an ONS survey to ensure the sample was representative of the wider population. From this sample 33 individuals in 30 households tested positive for COVID-19. This equates according to the ONS to 0.27% (95% confidence interval: 0.17% to 0.41%) of the population of England.
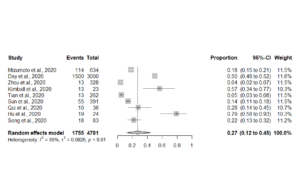
Secondly, one of the key problems with Covid-19 is asymptomatic spread (Bai et al., 2020) but there is no reliable data so any calculations here need to be looked on as a Fermi (back of an envelope) problem. To get a best estimate on the proportion of asymptomatic patients I conducted a meta-analysis of the data presented on the Oxford Covid-19 Evidence Service (Heneghan et al., 2020). The meta-analysis was carries out in R using a random effects model (See Figure 1.)
Figure 1. Forest plot of asymptomatic individuals
There are two points of note from this forest plot, the summary estimate for asymptomatic individuals is 27% (95%CI; 12 to 45%) and the heterogeneity between studies (variability) is extremely high.
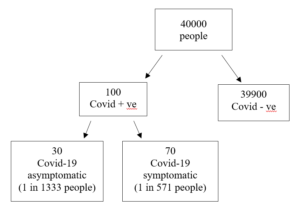
The next stage is to put the base-rate and number of asymptomatics together in the form of a frequency tree. For ease of calculation I have rounded the figures so a base-rate of 0.27% becomes 1 in 400, and the number of asymptomatics becomes 30% (See Figure 2.).
Figure 2. Frequency tree of asymptomatic vs symptomatic
The frequency tree illustrates that in this population 1 out of every 1333 people could be an asymptomatic carrier of Covid-19.
How does this relate to dentistry? On the precautionary principle we are operating under at the moment the presumption is that all (100%) the patients are asymptomatic carriers rather than the true figure of 0.075% ( I have assumed symptomatic patients will not be attending a dental surgery or will be triaged out prior to entering the clinical environment). This becomes important when we want to test if our PPE and protocols are effectively protecting both the patients and the staff. We now need to set up a study comparing PPE that is adequately powered to eliminate the effects of random chance around such a small prevalence statistic (Button et al., 2013). I have created three examples of PPE for aerosol generating procedures:
- Perfect PPE model (fluid resistant disposable gowns, FFP3 masks, visors, ventilation, long fallow periods etc) with a 99% chance of reducing viral contamination
- Realistic expectations of enhanced PPE practice (FFP2, reusable surgical gown, rubber dam etc) at 93%.
- Standard practice (surgical masks etc) at 80%.
I placed the data into an apriori sample size calculator (G*Power 3.19.2) with a error probability is 0.05 and power (1-b error probability) of 0.8 (See Table 1).
Table 1. Sample sizes for a well powered study into PPE effectiveness
| PPP protection level (%) | Sample size per arm
(Covid + ve) |
Total sample size
(Covid + ve) |
Total number of patient’s unknown diagnosis (n*prevalence) |
| 99.99 to 93.00 | 108 | 216 | 287,928 |
| 99.99 to 80.00 | 35 | 70 | 93,310 |
As we can see even in a simulation study, we are going to have to at least place over a hundred individuals in each arm of the study. To see if the benefit translates into the real-world, we need to go up two orders of magnitude to see if there is a significant difference between perfect and good PPE based on accurate population base-rate figures.
Discussion
The purpose of this opinion paper was to highlight the potential problems that a precautionary principle can create in healthcare when we work on the assumption that 100% of the patients attending a dental surgery are infectious. Guidelines and protocols need to take into consideration the absolute risk within the population based on data that is accurate and up to date. Simulation studies, and pilot studies rarely carry their full reported success into the real world (Kistin and Silverstein, 2015). Without taking a deep breath and objectively assessing the changing data regarding Covid-19, policy makers, academics, and clinicians can unconsciously fall fowl of the base-rate fallacy and availability biases created by the modern media. High quality PPE and staff training is a vital component of keeping everyone safe from this virus but we must be mindful of the other effects that perfect practice can have on the health economics and affordability of health care to those most vulnerable.
References
BAI, Y., YAO, L., WEI, T., TIAN, F., JIN, D. Y., CHEN, L. & WANG, M. 2020. Presumed Asymptomatic Carrier Transmission of COVID-19. JAMA.
BASTIAN, H. 2020. A rebuttal to “A fiasco in the making?” [Online]. Available: [Accessed 17th May 2020].
BUTTON, K. S., IOANNIDIS, J. P., MOKRYSZ, C., NOSEK, B. A., FLINT, J., ROBINSON, E. S. & MUNAFÒ, M. R. 2013. Power failure: why small sample size undermines the reliability of neuroscience. Nature Reviews Neuroscience, 14, 365-376.
CHAMBERS, D. W. 1999. The roles of evidence and the baseline in dental decision making. J Am Coll Dent, 66, 60-7.
GAURAV, S. 2020. Behavioural Economics in the Fight Against COVID-19: BOMA Framework. [Accessed 17th May 2020].
HENEGHAN, C., BRASSEY, C. & JEFFERSON, T. 2020. COVID-19: What proportion are asymptomatic? [Online]. Available: [17th May 2020].
IOANNIDIS, J. P. 2020. A fiasco in the making? As the coronavirus pandemic takes hold, we are making decisions without reliable data [Online]. STAT. Available: [17th May 2020].
KISTIN, C. & SILVERSTEIN, M. 2015. Pilot studies: a critical but potentially misused component of interventional research. JAMA, 314, 1561-1562.
ONS. 2020. Coronavirus (COVID-19) Infection Survey pilot: England, 14 May 2020 [Online]. Available: [17th May 2020].
TALEB, N. 2020. EVIDENCE BASED is often BS [Online]. Available: [17th May 2020].
Picture Credits
“Personal Protective Equipment” by National Institutes of Health (NIH) is licensed under CC BY-NC 2.0

[…] Are we sleepwalking into PPE paralysis? […]
Thank you very much for your great article and research, putting our PPE efforts and requirements into perspective. With effective screening for symptoms and reasonably low prevalence in a geographical area the risk of seeing an asymptomatic patient is certainly expected to be very low, which is important for the individual practitioner and assistant.
Two thoughts are currently motivating me to be extra-vigilant with respect to measures in the clinic:
– An uncertain percentage of pre-symptomatic transmission (Studies mention between 13% and 46%)
– An extremely skewed risk profile with respect to public perception. Even though the risk of an infection in a dental clinic of a health care worker or patient is very low, the impact of a possible transmission could be dramatic, should just one case be confirmed and made public. Public opinion currently seems to be heavily affected by “anecdotal evidence”, and one reported case could possibly put the dental world in a defensive position. Elevated PPE to follow along with public sentiment could provide some insurance.